CS16, Summer 2012

Lab05:
Functions

---

Goals for this lab

By the time you have completed this lab, you should be able to

• Write C functions
• Test functions with ch
• Use your functions in C programs

Step by Step Instructions

Step 1: Get together with your lab partner, and create a lab05 directory

Choose the first partner wisely (Lab04, Step 0 explained the goal). If your assigned partner is more than 5 minutes late, ask the TA to pair you with someone else for this week.

This lab's first pilot should log in, create ~/cs16/lab05/ and make that your current directory.

Step 2: Practice writing and testing small functions at the ch prompt

Start ch, and simplify the ch prompt if you want:

-bash-4.2$ ch
                                   Ch
                Professional edition, version 6.1.0.13751
              (C) Copyright 2001-2009 SoftIntegration, Inc.
                     http://www.softintegration.com
/cs/class/cs16/lab05> _prompt = "ch> "
ch>
ch>

Type (or copy/paste) the function below, void f1(void), all on one line at the ch prompt. By the way, here is the function described in words like instructions below for functions that you will create yourself:

Write a function named f1 that takes no arguments, and has a return type of void. It should print "f1 running" and a newline.

Then test it:

ch> void f1(void) { printf("f1 running\n"); }
ch> f1()
f1 running

If you made a mistake or just want to change something, you can't just redefine the function. Notice what will happen if you try:

ch> void f1(void) { printf("f1 running differently\n"); }
ERROR: redefine the user-defined procedure body for 'f1'

Instead you have to use the ch command remvar as in:

ch> remvar f1
ch> void f1(void) { printf("f1 running differently\n"); }
ch> f1()
f1 running differently

Now you write one that takes an argument and returns a value.

Write a function (all on one line) named f2 that takes one int argument named x, and returns a double value equal to 1.0/x (the multiplicative inverse of x). Do NOT print anything.

Type this function definition at the ch prompt. Then test it a few times:

ch> CENSORED: FUNCTION DEFINITION HERE
ch> f2(100)
0.0100
ch> f2(0)
inf
ch> double answer = f2(25);
ch> answer
0.0400
ch>

Notice in the last test above, how the function returns an answer without printing anything - in this test, the answer is stored in a variable and shown later. Also notice the special value ch printed when the function tried to calculate 1.0/0 and keep this behavior in mind.

Step 3: Write and test a longer function with a ch "function file"

It is possible, but awkward to type functions longer than one line at the ch prompt (using the "continuation character" we used in Lab03 for selection structures), but ch provides a much better way.

If you create a file with .chf as the extension, and the first part of this file's name exactly matches the name of the function (to be used externally), and the file is stored in the current directory (or elsewhere in _fpath), then you can execute the function at the ch prompt.

Use emacs or another editor to create a file named dfactorial.chf. [Note you don't have to exit ch to start the editor.] Type a comment such as /* calculates factorial of n as double */ on the first line. Then define a function to find n factorial as a double value. In case you never heard of it, or you forgot its definition, n factorial is abbreviated as n! and it is defined as follows:

n! = (n)(n-1)...(2)(1)

where n is a non-negative integer, and 0! = 1. So, for example:

5! = 5*4*3*2*1 = 120

Type the function definition after the comment. Here are the specific instructions:

Write a function named dfactorial that takes one int argument named n, and returns a double value that is equal to n factorial.

Save the file as dfactorial.chf in the lab05 directory.

Then test it from the ch prompt. If something doesn't work correctly, then fix the problem before going to Step 4. Here are some correct answers to expect:

ch> dfactorial(5)
120.0000
ch> dfactorial(10)
3628800.0000
ch> dfactorial(50)
30414093201713375576366966406747986832057064836514787179557289984.0000
ch> printf("%g", dfactorial(50))
3.04141e+64

Step 4: Find out your function's limits

First: switch roles between pilot and navigator if you did not already do that.

Of course you noticed that 50! is a very large number, but apparently it still is well within the range of the double data type. What value results when you plug in 200 for n? Now we want you to experiment a bit.

1. Devise a way to find out the largest value of n for which dfactorial(n) returns an accurate value.
2. Find this largest value, and remember it to use for Step 5 (also to tell your TA if they ask later).
3. You should also know that ch includes a built-in function named factorial that returns a long long int. Find out the maximum value you can plug into that built-in function, and also note what it returns when it receives a larger value. Interesting? Appropriate?

Step 5: Write and test a program to approximate e

Here, e refers to the mathematical constant that is the base of natural logarithms. Like π and other such constants, this number is irrational, and so it can only be approximated (2.71828183 is a usable approximation, but nevermind that for now).

One way to define the true value of e is the sum of an infinite series of multiplicative inverses of factorials:

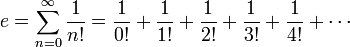Recall that 0! is 1, so this series begins with 1 + 1, its third term is 1/2! (= 1/2), its fourth term is 1/3! (= 1/6), and so on. Of course you can't write a program to calculate an infinite series, and besides that you know your factorial function has a largest value for which it works correctly (which is larger than the built-in function, but still not infinity!).

Write a C program that contains a copy of your dfactorial function, and a new main function that uses it to approximate and print the value of e. First exit ch, then accomplish the following steps:

1. Make a copy of dfactorial.chf named e.c:

   -bash-4.2$ cp dfactorial.chf e.c

2. Edit the copy with emacs or another editor:

   -bash-4.2$ emacs e.c

3. Type a C comment at the top of the file - above the dfactorial function - with a very brief description of the program you are creating, plus your name(s) and the date.
4. Type a blank line after the comment. Then type the C preprocessor command that includes the C standard input-output library, and then another blank line - all above the existing function.
5. Now skip down to below the dfactorial function, and begin the main function as usual. You might as well terminate main now too, and include the following features inside its brackets (curly braces):
   1. Declare a double variable named e, and initialize it to 1. Also declare an integer variable named n which will be used for loop control, and for passing to dfactorial.
   2. Begin a loop in which the value of n will vary from 1 to the maximum value that can be passed to your dfactorial function (see Step 4 above).
   3. Inside the body of the loop, use the variable e to accumulate the sum of terms necessary to approximate e (i.e., add 1/n! to the current value of e on each iteration).
   4. After the loop, print the value of e with at least 8 digits of precision after the decimal point, and with a nice label, as in the example run below from our solution.
   5. Exit normally.

You can use ch to test your program. Then make an executable version of it:

-bash-4.2$ make e
cc     e.c   -o e
-bash-4.2$ ./e
e is approximately 2.71828183

Step 6: Show off your work and get credit for the lab

Submit your lab with the turnin program. You MUST have both your name and your partner's name in the files in order to receive credit. Remember that the original pilot needs to do this step, since that is whose account you have been using in Cooper Lab.

Bring up a terminal window on CSIL, and cd into the original pilot's cs16 directory, and cd again into the lab05 directory. Then type the following to turn in both files that you created in Steps 3 and 5 above:

turnin lab05@cs16 dfactorial.chf e.c

Respond "yes" when the program asks if you want to turn in (be sure to read the list of files you are turning in), and then wait for the message indicating success.

---

Evaluation and Grading

Each student must accomplish the following to earn full credit for this lab:

• Turn in a complete and accurate pre-lab #5 - should have done at the beginning of lab.
• dfactorial.chf is saved, and it executes properly with ch.
• e.c is saved, and it compiles and executes properly.
• dfactorial.chf and e.c have been turned in.
• If a pair completes the above tasks early, they must work the entire lab period by attempting the extra challenge problems below.

Deadline for lab submission: Wednesday, August 1 (11:59pm)

---

Optional Extra Challenge

• Convert the statements that approximate e (in Step 5) to a function. Then you can greatly simplify the main function to just print the results of this new one.
• In truth, your program does not really have to add terms all the way to the maximum factorial value that can be calculated by your Step 3 function. In fact, a much shorter series will achieve a result that is accurate to 8 digits. Devise a way, and find out the maximum value of n that is necessary to achieve this accuracy.
• Perhaps you experimented to find the answer to the previous challenge. Another way to approach problems like this one is to check how much the approximation changes each iteration, and stop iterating when this change is negligible (very nearly 0). Try that approach.
• The exponential function e^x may be defined by a very similar infinite series of terms: Write a function to calculate it. Then write a program that asks the user to enter a value of x, and prints e^x with a nice label.

---

Adapted by Kyle Dewey from a lab prepared by Michael Costanzo.