NOTE: these proof examples use rules related to negation, true, and false. The handout presented in lecture lacks these rules, as the rules are completely redundant with other rules. That is, adding explicit rules for negation, truth, and falsehood does not make the logic any more powerful (read: there is nothing that cannot be expressed without these rules). However, it can make proofs more convenient. The rules for negation, true, and false can be seen in this slightly modified handout.
First, a proof that p => !!p, which in the logic we are using (intuitionistic logic) corresponds to saying “if I have a proof of p, then I can prove that it's impossible to prove that p is false” (i.e., if I have something then I can prove that it's impossible to prove that the thing does not exist).
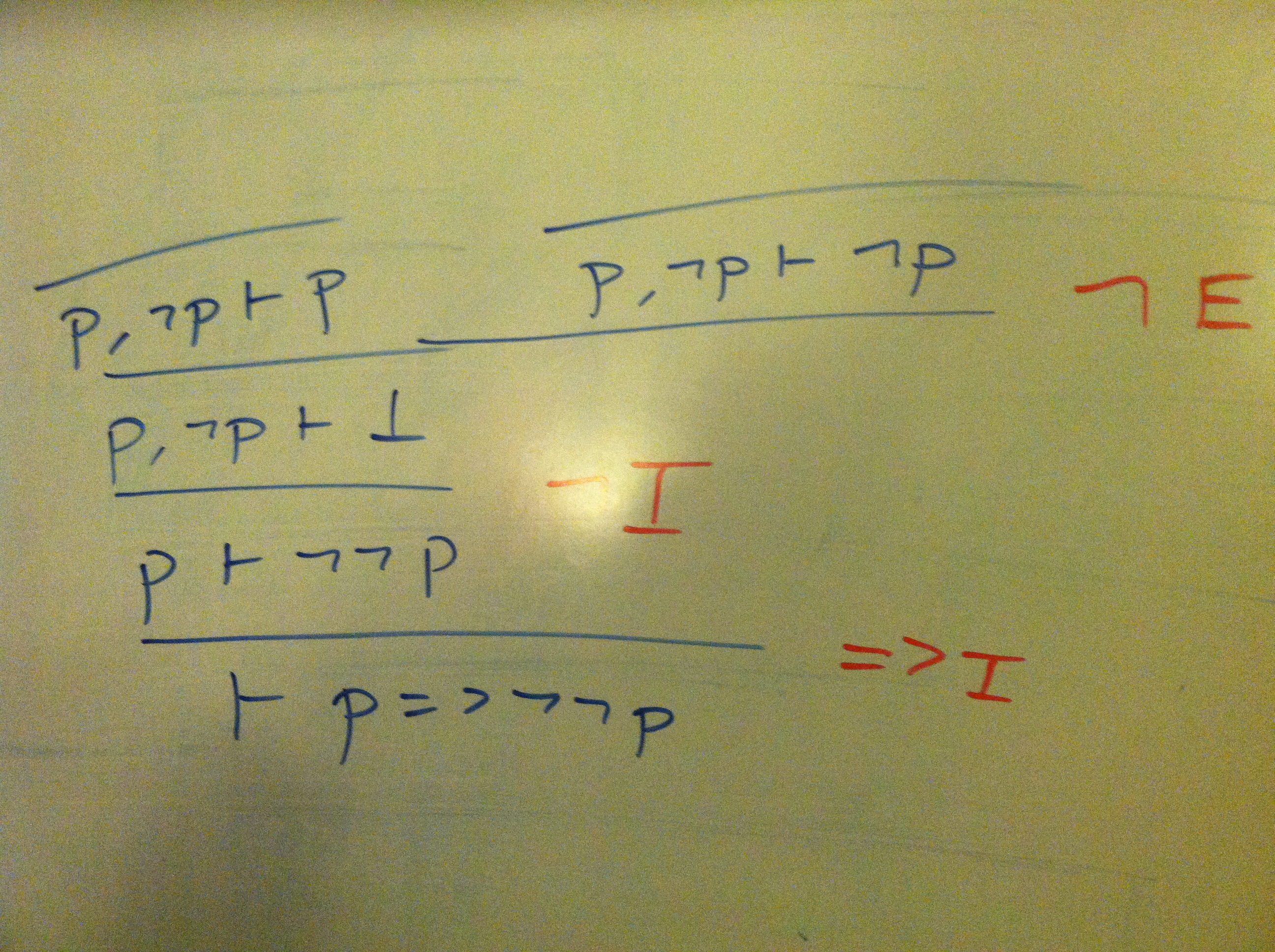
Now a more interesting proof: in classical logic, it is true that p => q itself implies that !p || q.
First, we will add in additional rules for double negation (which are found in classical logic, but not intuitionistic logic):
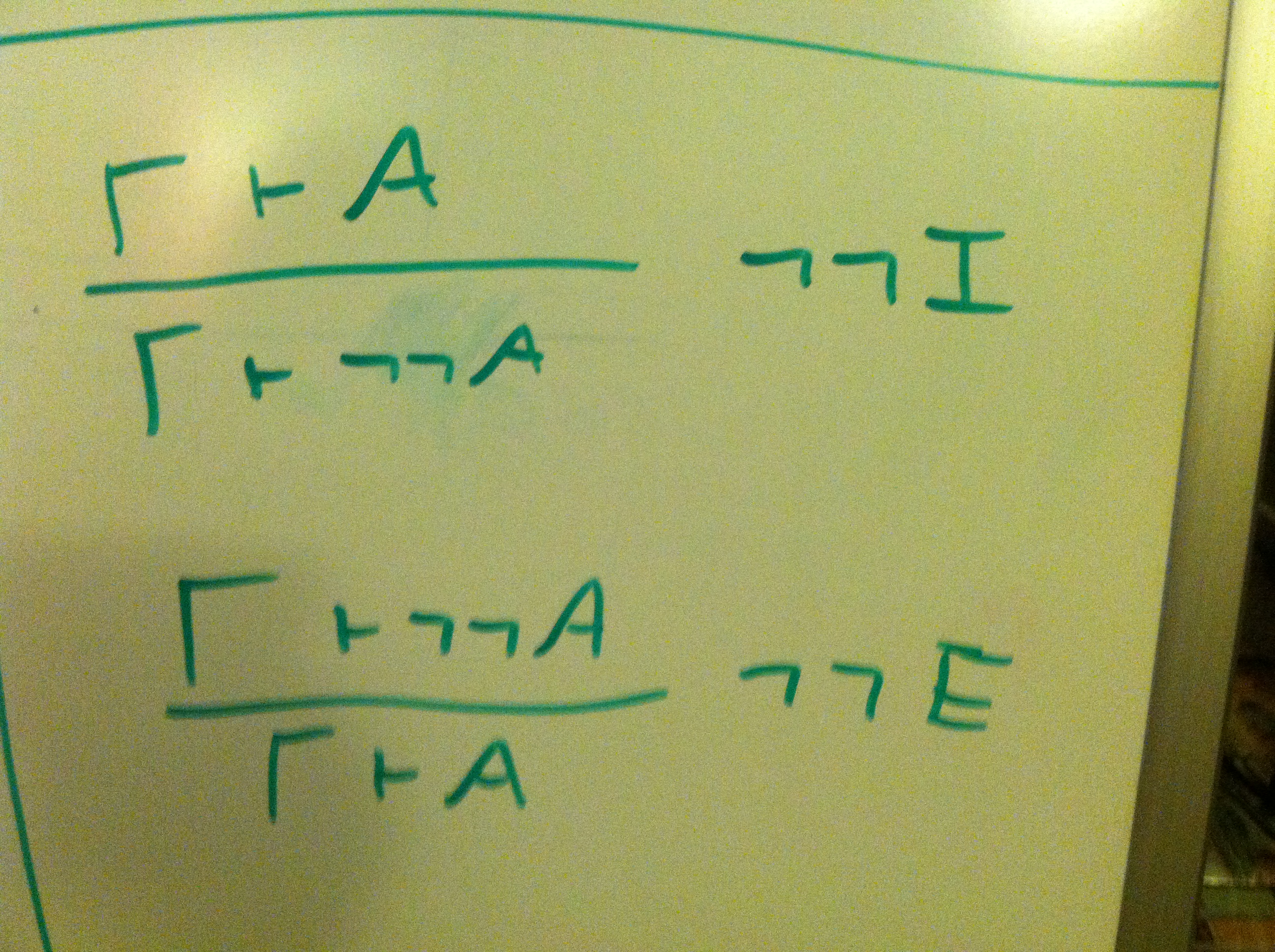
For the sake of brevity, I use two variables, gamma and gamma prime, to represent two different sets of assumptions. These are shown below:
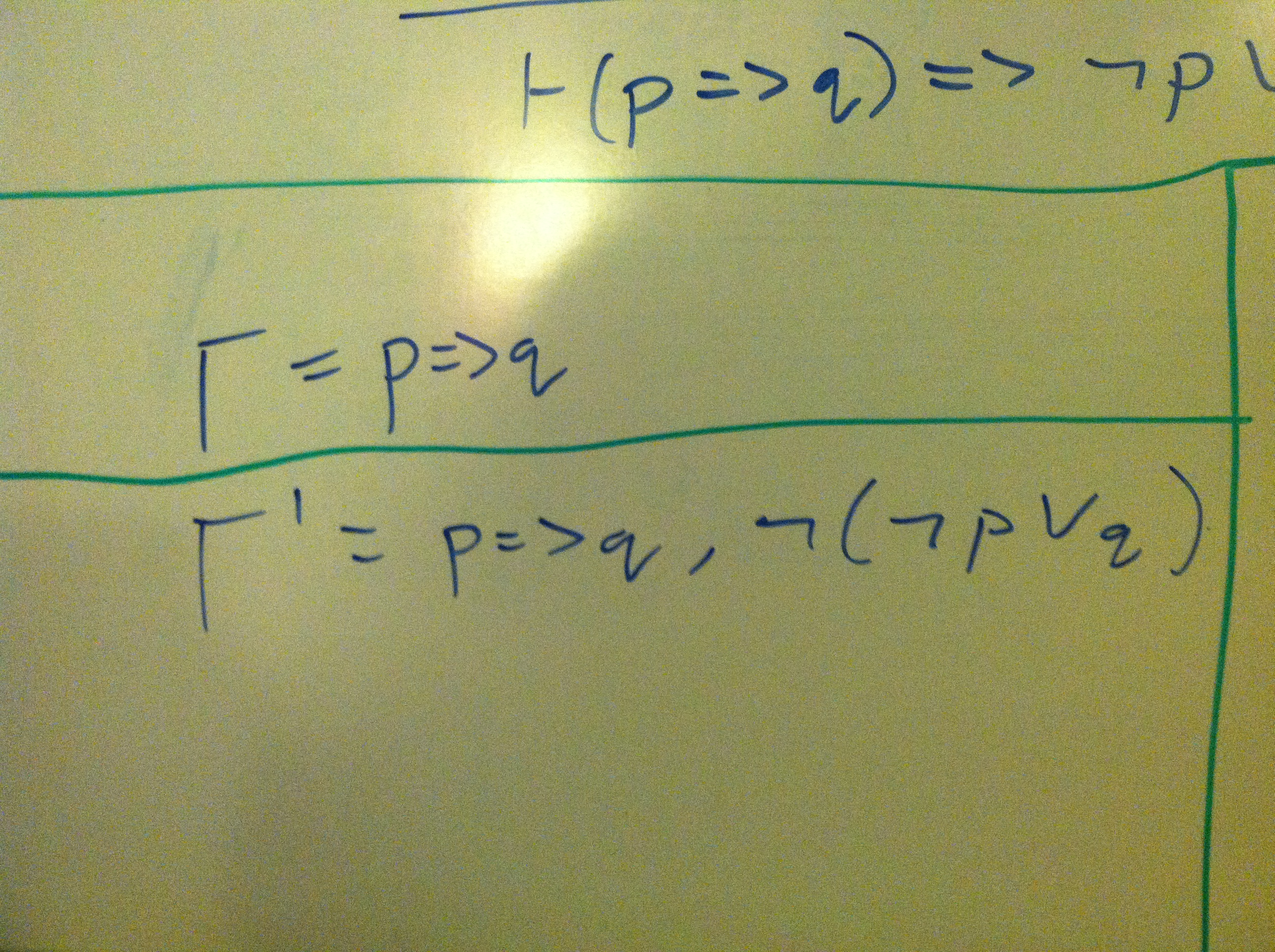
Putting it altogether, the proof is below:

Note that the rules for double negation (corresponding to classical logic) are required for this proof, and that this statement isn't actually true in intuitionistic logic (which is what the handout is based on).