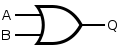
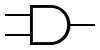

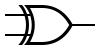
!A refers to the negation of variable A, and so on:
R = !A!B + AB
R = !ABC + ABC + A!B!C
Using the above equation, do the following:
- Write it as a truth table
- Simplify it using boolean algebra
- Simplify it using a Karnaugh map
The exam will consist of short-answer questions and writing your own code. A significant portion will consist of writing code (more than half the points), so you should be prepared to do this.
The review below, in addition to Lab 4, Lab 5, and Lab 6, are all fair game for the exam. For the labs, this includes both code you've written and questions you've answered. Between this review and the aforementioned three labs, this information is intended to be comprehensive; there will be no material on the exam which isn't touched by either the labs or this review.
If you're pushed for time, my personal recommendation is to spend the majority of your time studying what you wrote for your labs, both code and questions. You'll find the review below to be largely (though not entirely) redundant with that information.
$t0 - $t9.
You may assume that the C types int, unsigned int, and int* are each 32 bits long.
int s0 = 0;
unsigned int s1;
// `s1` and `s2` are of type `unsigned int`
// `s3` is of type `int*`
for (s1 = 0; s1 < s2; s1++) {
s0 = s0 + s3[s1];
}
$t0 - $t9.
You may assume that the C types int, unsigned int, and int* are each 32 bits long.
You may assume that array was declared globally, and it is an array of unsigned int.
array[0] = 0;
array[1] = 1;
unsigned int s0;
for (s0 = 2; s0 <= s1; s0++) {
array[s0] = array[s0 - 1] + array[s0 - 2];
}
s2 = array[s1];
myArray (which is declared elsewhere, and is of length 10), and do something with each element:
# initialize registers move $t0, $zero li $t1, 10 loop: # check that we're still in the loop slt $t2, $t0, $t1 beq $t2, $zero, after_loop # load myArray[$t0] into $t5 la $t3, myArray add $t4, $t3, $t2 lw $t5, 0($t4) # do something with myArray[$t0], AKA $t5. # this has been omitted # increment counter and go back to the top addiu $t0, $t0, 1 j loop after_loop: # this is where code after the loop goes
The code above has a bug in it which will cause it not to iterate through the loop correctly.
Specifically, $t3 won't always hold the value of myArray[$t3].
Two questions follow:
You should be familiar with the rules in the MIPS calling convention documentation. The following questions all indirectly relate to that document.
li $t0, 10 # save 10 into $t0 jal foo # call foo add $t1, $t0, $t0 # 10 + 10 = 20
int add2(int x, int y) {
return x + y;
}
Answer the following questions, which are all related to how the above code behaves with respect to the MIPS calling convention:
add2 is called, in what registers will the values of x and y be initially placed?add2 returns, in what register will its return value (x + y) be placed?bar below is implemented in MIPS assembly, which takes two parameters, which we'll name x and y, respectively.
The function is supposed to return the result of (x * y) - (x + y).
However, there is a bug in the function, with respect to the MIPS calling convention.
What's wrong with the code, and how could it be fixed?
bar: mult $a0, $a1 mflo $s0 add $s1, $a0, $a1 sub $v0, $s0, $s1 jr $ra
first, below, which calls another function second.
second doesn't take any parameters, and it doesn't return anything.
There is a bug in the code below.
What's wrong with the code, and how could it be fixed?
first: jal second jr $ra
third, below, which calls another function fourth.
fourth doesn't take any parameters, and it doesn't return anything.
There is a bug in the code below.
What's wrong with the code, and how could it be fixed?
third: addiu $sp, $sp, -4 sw $ra, 0($sp) jal fourth lw $ra, 0($sp) jr $ra
$t0 needs to be maintained through a call, but we're constrained in that we're not allowed to store $t0's value in a preserved register (e.g., $s0 - $s7).
This can't be done directly, as the MIPS calling convention allows the caller to clobber $t0.
However, there is still a way to save the value of $t0 somewhere where it can survive the call, without needing to use a preserved register.
Where can $t0 be saved?
How can this be done, specifically with valid MIPS assembly which obeys the MIPS calling convention?
simple_call.asmprint_ints.asmadd_ints.asmsave_registers.asmnested_calls.asmrecursive_fibonacci.asmYou will not be asked about tail-recursion.




!A refers to the negation of variable A, and so on:
R = !A!B + AB
R = !ABC + ABC + A!B!C
Using the above equation, do the following: