Due Monday, December 7 at 11:59:59 PM
By the time you have completed this work, you should be able to:
For this week, you will translate a word problem into a diagram representing a finite state machine (FSM). From there, you will provide enough detail to implement the finite state machine as a circuit. There are multiple tasks for this assignment. While each task can be completed independently of each other, they progressively build in difficulty, so it is recommended to complete them in order. The tasks are listed below:
010110The initial step below describes how to get the files you will need into the appropriate place. These files are used for all the different tasks.
After you log in, go into your cs64 directory that you created last time:
cd cs64
Then create a new directory for this lab: lab9:
mkdir lab9
Then go into that directory.
Now copy over all of the files necessary for this week's tasks:
cp ~kyledewey/public_html/cs64/labs/9/partner.txt .
Note the use of the trailing . in the above command, which stipulates that the specified files should be copied into the current directory.
In this task, you will design a FSM which controls a seven segment display. Throughout this task, we will be using a seven segment display similar to the following (provided by Wikipedia):
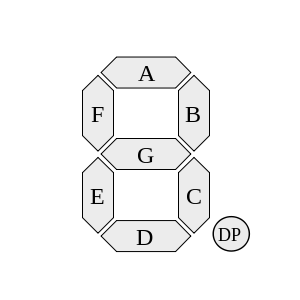
Each of the letters in the above diagram refers to an individual segment of the display.
The identifier “DP” refers to the decimal point, which will not be used in this task.
The display allows segments to be individiually turned on and off, allowing for different numbers to be represented by selectively enabling or disabling the right segments.
The table below illustrates which segments need to be enabled for the corresponding decimal digit to be represented:
| Number | Segments to Enable |
|---|---|
0 |
A, B, C, D, E, F |
1 |
B, C |
2 |
A, B, G, E, D |
3 |
A, B, G, C, D |
4 |
F, B, G, C |
5 |
A, F, G, C, D |
6 |
A, F, G, E, C, D |
7 |
A, B, C |
8 |
A, B, C, D, E, F, G |
9 |
A, B, C, D, F, G |
The FSM for this task should alternate between displaying 1, 2, 4, and 8, in that order.
In order to accomplish this, the inputs to the seven segment display will be treated as outputs of your FSM.
That is, your FSM will output the appropriate values of A, B, C, D, E, F, and G in order to represent the numbers of interest.
This overall task is separated into a series of questions, which may be submitted in the CS64 homework box (in Harold Frank Hall, room 2108), or digitally via the turnin command.
Draw the finite state machine corresponding to this task.
If you are submitting this online, put this diagram into a file named “display.jpg”.
How many latches/flip-flops do you need to implement this state machine?
(Hint: this corresponds to the number of bits necessary in order to encode all possible states uniquely.)
If you are submitting this online, put this into a file named “display.txt”.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Draw a single truth table representing the behavior of the state machine.
Be sure to label your states in binary.
Your table should have inputs corresponding to whatever state you are in.
The output corresponds to the next state to enter for a given input state, along with the values for the seven segment display.
If you are submitting this online, add this to your “display.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Using a Karnaugh map, determine the minimal sum-of-products formula corresponding to output A (corresponding to input A of the seven-segment display.
Where appropriate, use don't cares in the map (note that there may be no appropriate uses of don't cares).
If you are submitting this online, add this to your “display.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Using a Karnaugh map, determine the minimal sum-of-products formula corresponding to the rightmost bit of the next state.
Where appropriate, use don't cares in the map (note that there may be no appropriate uses of don't cares).
If you are submitting this online, add this to your “display.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
To help with questions 1-3, a solution to a very similar problem is provided here.
In this example, the FSM alternates between displaying 1 and 7.
The diagram has these major components:
1 or a 7.
7 (binary 1), the output of the state is ABC, meaning segments A, B, and C in the seven-segment display should be activated.
In conjunction, when these three segments are lit up, they display 7.
01
In this task, you will design a FSM which will set a particular output U to 1 each time 01 is encountered in a stream of inputs.
Inputs are specified one at a time, and are represented by the variable I.
To illustrate, consider the following example, which shows different values of U and I over time, where each cell is separated by a clock tick:
I |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
U |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
In the above example, it may appear that the output of U is delayed with respect to input I.
That is, when the 1 is 01 is encountered, it's not until the next clock tick that U is set to 1.
This is actually expected behavior, as it reflects the fact that first the circuit reads 1, and then it moves into a state that reports U = 1.
The key difference between this task and Task 1 is that this circuit takes an auxilliary input, which changes over time. As such, the finite state machine diagrams you draw should reflect changes in behavior, depending on which inputs are provided. Ultimately, this means that your FSMs will transition to different states depending on the inputs provided.
This overall task is separated into a series of questions, which may be submitted in the CS64 homework box (in Harold Frank Hall, room 2108), or digitally via the turnin command.
Draw the finite state machine corresponding to this task.
If you are submitting this online, put this diagram into a file named “sequence1.jpg”.
How many latches/flip-flops do you need to implement this state machine?
(Hint: this corresponds to the number of bits necessary in order to encode all possible states uniquely.)
If you are submitting this online, put this into a file named “sequence1.txt”.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Draw a single truth table representing the behavior of the state machine.
Be sure to label your states in binary.
Your table should have inputs corresponding to whatever state you are in, along with I.
The output corresponds to the next state to enter for a given input state, along with U.
If you are submitting this online, add this to your “sequence1.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Using a Karnaugh map, determine the minimal sum-of-products formula corresponding to output U.
Where appropriate, use don't cares in the map (note that there may be no appropriate uses of don't cares).
If you are submitting this online, add this to your “sequence1.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Using a Karnaugh map, determine the minimal sum-of-products formula corresponding to the rightmost bit of the next state.
Where appropriate, use don't cares in the map (note that there may be no appropriate uses of don't cares).
If you are submitting this online, add this to your “sequence1.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
To help with questions 1-3, a solution to a very similar problem is provided.
The state diagram is here, and the corresponding truth table is here.
The only difference between Task 2 and this provided solution is that the provided solution recognizes 10 as opposed to 01.
0110
In this task, you will design a FSM which will set a particular output U to 1 each time 0110 is encountered in a stream of inputs.
Inputs are specified one at a time, and are represented by the variable I.
To illustrate, consider the following example, which shows different values of U and I over time, where each cell is separated by a clock tick:
I |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
U |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
In the above example, it may appear that the output of U is delayed with respect to input I.
That is, when the 1 is 0110 is encountered, it's not until the next clock tick that U is set to 1.
This is actually expected behavior, as it reflects the fact that first the circuit reads 1, and then it moves into a state that reports U = 1.
This overall task is separated into a series of questions, which may be submitted in the CS64 homework box (in Harold Frank Hall, room 2108):
Draw the finite state machine corresponding to this task.
If you are submitting this online, put this diagram ito a file named “sequence2.jpg”.
How many latches/flip-flops do you need to implement this state machine?
(Hint: this corresponds to the number of bits necessary in order to encode all possible states uniquely.)
If you are submitting this online, put this into a file named “sequence2.txt”.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Draw a single truth table representing the behavior of the state machine.
Be sure to label your states in binary.
Your table should have inputs corresponding to whatever state you are in, along with I.
The output corresponds to the next state to enter for a given input state, along with U.
If you are submitting this online, add this to your “sequence2.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Using a Karnaugh map, determine the minimal sum-of-products formula corresponding to output U.
Where appropriate, use don't cares in the map (note that there may be no appropriate uses of don't cares).
If you are submitting this online, add this to your “sequence2.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Using a Karnaugh map, determine the minimal sum-of-products formula corresponding to the rightmost bit of the next state.
Where appropriate, use don't cares in the map (note that there may be no appropriate uses of don't cares).
If you are submitting this online, add this to your “sequence2.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Note the similarity between this task and Task 2. Task 3 ends up doing something very similar to both Task 2 and the example solution provided for the task similar to Task 2. That said, be sure to take into account the differences. Pay particularly close attention to where transitions should go which move “backwards” in the FSM. That is, it is expected that you'll have transitions which go to previously observed states, and these transitions won't necessarily all return to the same state.
In this task, you will design a FSM for a simple (albeit strange) vending machine of office supplies. The vending machine sells three possible items, each at a different cost:
| Item | Cost |
|---|---|
| Pencil | 10 cents |
| Eraser | 20 cents |
| Pen | 30 cents |
The vending machines accepts nickels (worth 5 cents), dimes (worth 10 cents), and quarters (worth 25 cents).
Physically, it is only possible to insert a single coin at a time.
The vending machine features a large button labeled “DONE”, which, when pressed, will dispense the most expensive item which can be purchased with the input money.
For example, if a dime and two nickels had been entered (totalling 20 cents), then it would dispense an eraser upon pressing “DONE”.
Once an item is dispensed, the vending machine returns to an initial state wherein it shows that no money has been inserted.
To help simplify things, the vending machine does not provide any change.
This means that any additional money provided will be lost.
For example, if a quarter had been entered and then “DONE” pressed, the vending machine would dispense an eraser (because this is the most expensive item which can be purchased with 25 cents), and then the vending machine would return to the point where it shows that no money has been entered.
As another example, if two quarters had been entered, then upon pressing “DONE”, it would dispense a pen (the most expensive item purchasable with 50 cents), and then the vending machine would return to the point where it shows that no money has been entered.
While there are different ways to model these different parameters as inputs, your FSM should deal with the following inputs:
| Input | Description |
|---|---|
K |
Set to 1 if a nickel has been entered, else 0 |
D |
Set to 1 if a dime has been entered, else 0 |
Q |
Set to 1 if a quarter has been entered, else 0 |
E |
Set to 1 if “DONE” has been pressed, else 0 |
In addition to the above inputs, you'll also need to specify what the current state is, which should be indicated with inputs C0 through CN, where N is the position of the greatest possible bit in your state encoding.
For example, if you needed eight states in your FSM, then you'd have inputs C0, C1, and C2, as eight states can be uniquely encoded using three bits.
Similarly to the inputs, the output parameters can be modeled in different ways. However, for the sake of consistency across different solutions, your FSM should deal only with the following outputs:
| Output | Description |
|---|---|
DPENCIL |
Short for “Dispense Pencil”.
Set to 1 if we should dispense a pencil, else 0.
|
DERASER |
Short for “Dispense Eraser”.
Set to 1 if we should dispense an eraser, else 0.
|
DPEN |
Short for “Dispense Pen”.
Set to 1 if we should dispense a pen, else 0.
|
In addition to the above outputs, you'll also need to specify what the next state is, which should be indicated with outputs N0 through NM, where M is the position of the greatest possible bit in your state encoding.
For example, if you needed eight states in your FSM, then you'd have inputs N0, N1, and N2, as eight states can be uniquely encoded using three bits.
This overall task is separated into a series of questions, which may be submitted in the CS64 homework box (in Harold Frank Hall, room 2108):
Draw the finite state machine corresponding to this task.
If you are submitting this online, put this diagram ito a file named “vending.jpg”.
How many latches/flip-flops do you need to implement this state machine?
(Hint: this corresponds to the number of bits necessary in order to encode all possible states uniquely.)
If you are submitting this online, put this into a file named “vending.txt”.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
Draw a single truth table representing the behavior of the state machine.
Be sure to label your states in binary.
Your table should have inputs and outputs corresponding to the inputs and outputs described previously.
If you are submitting this online, add this to your “vending.txt” file.
This will be read by hand, so don't worry about the formatting (as long as it is clear and unambiguous).
To simplify things, you may put don't cares where appoproiate in the inputs.
For example, because it is physically impossible to insert more than a single coin at a time, if input K = 1 (indicating a nickel has been inserted), then inputs D and Q can be safely labeled as don't cares, as implicitly they should always be 0 (and in reality we ignore their values entirely in this situation).
With this setup, we can cut down on the number of repeated rows; instead of having two rows which differ in only whether or not Q is set, we can have a single row where Q = X.
The following are a series of hints which may be of use while implementing Task 4:
You may assume only one coin is ever entered at a time.
For example, this means that if D = 1 (indicating a dime was entered), then it is guaranteed that K = 0 and Q = 0 (indicating a nickel and a quarter were not entered, respectively).
Similarly, you don't need to worry about the user inputting multiples of the same coin at once (e.g., two quarters at once), which does not have a possible encoding in this setup.
The practical advantage of this assumption is that transitions will only ever depend on one input at a time; you'll never need a transition which corresponds to the user inputting a combination of coins.
You may assume that “DONE” is pressed only after all coins have been entered.
Similar to the previous assumption, this means you don't need to worry about a case where the user inputs a coin while simultaneously pressing “DONE”.
For example, if E = 1, then it is guaranteed that K = 0 (meaning no nickels were inserted).
You may assume that when “DONE” is pressed, the user will provide no more input until the vending machine has finished dispensing the most expensive item purchasable with the input money.
This means that until the vending machine returns to the original state it started in with no input money, K = 0, D = 0, Q = 0, and E = 0.
You may assume that the vending machine does not provide any change, and gives no indication to the user when money has simply been eaten.
As with the example before, this means that if more money was provided than needed (e.g., providing 25 cents to purchase a 20 cent eraser), then the additional money simply disappears.
Similarly, if the user does not provide enough money to purchase anything (e.g., inserting only a nickel and subsequently pressing “DONE”), then no items should be dispensed, but the vending machine will still return to the initial state.
To help keep your diagrams clean, you need only indicate outputs when the output would be 1.
For example, if in one particular state a pencil should be dispensed, then in this particular state DPENCIL should be indicated.
In all other states, simply omitting DPENCIL is equivalent to outputting that DPENCIL = 0.
As for what your states in this vending machine indicate, probably the simplest approach is to have a distinct state for each amount of currency which can be deposited. At the very least, this means having states corresponding to 5 cents deposited, 10 cents deposited, 15 cents deposited, and so on. While your vending machine will likely need more states than this, the bulk of the states work in this fashion.
Technically, a user can input an arbitrarily large amount of money into the machine. However, you don't need to worry about this too much, as the vending machine only dispenses one item at a time, and provides no change. As such, inputting 30 cents (enough to buy a pen, the most expensive item), is no different than inputting 35 cents or more.
turnin, or the CS64 Homework Box
If you partnered with someone, record the email address they are using for the class in partner.txt.
For example, if your partner had the email address foo@bar.com, then the contents of partner.txt should be the following (and only the following):
Partner: foo@bar.com
If you did not partner with anyone, you do not need to (and should not) edit partner.txt.
Assuming you are in the cs64/lab9 directory you created at the beginning, you can send in your answers with the FSM images and answers via the following command:
turnin lab9@cs64 display.jpg display.txt sequence1.jpg sequence1.txt sequence2.jpg sequence2.txt vending.jpg vending.txt
If, instead, you are planning to turn in the image using the CS64 homework box in Harold Frank Hall, room 2108, then you can use the following command:
turnin lab9@cs64 partner.txt
You may turn in the same assignment up to 100 times, which is useful if you are working on it incrementally. Note that only the last version you submitted will be graded.
Even if you did not partner with anyone, you should still turn in partner.txt, which should not have been modified.
Prepared for Computer Science 64 by Diana Franklin, with some adaptation by Kyle Dewey.