| A | B | C | D | U |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 |
Using the above truth table, write out the following:
- The unoptimized sum-of-products equation, skipping over don't cares
- A Karnaugh map, along with boxes which exploit don't cares where appropriate
- An optimized sum-of-products equation, derived from the Karnaugh map created in the previous step
Design a two-bit arithmetic logic unit (ALU) that has the following operations:
- Add the two operands together
ANDthe two operands togetherORthe two operands togetherXORthe two operands together
Specifically, your ALU will have the following inputs:
| Input Name | Input Description |
|---|---|
A0 |
Bit 0 of the first operand |
A1 |
Bit 1 of the first operand |
B0 |
Bit 0 of the second operand |
B1 |
Bit 1 of the second operand |
S0 |
Select bit 0, used for specifying the operation to perform (see table below) |
S1 |
Select bit 1, used for specifying the operation to perform (see table below) |
As for which operation should be performed, this is based on the values of inputs S0 and S1.
The table below described the values that correspond to the different operations:
Value for S0 |
Value for S1 |
Operation |
|---|---|---|
0 |
0 |
Addition |
0 |
1 |
AND |
1 |
0 |
OR |
1 |
1 |
XOR |
For this task, you may use the following provided components, in unlimited supply:
- AND, OR, XOR, and NOT gates
-
Single bit adders, which take the operands to work with (
I1andI2), along with a carry-in (CI). These produce a carry-out bit (CO), along with a result bit (R). These are denoted with the following symbol: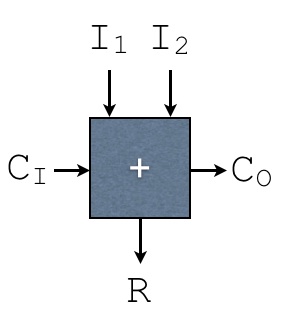
-
2-input multiplexers, which take a selector bit
S0and two single-bit input operandsAandB, and return a single-bit outputZ. They should be drawn using the symbol below, provided by Wikipedia: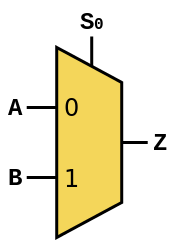
Design a finite state machine (FSM) which will set a particular output U to 1 each time 1001 is encountered in a stream of inputs.
Inputs are specified one at a time, and are represented by the variable I.
To illustrate, consider the following example, which shows different values of U and I over time, where each cell is separated by a clock tick:
I |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
U |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
For this task, you should be able to:
- Draw the FSM
- Define how many latches/flip-flops are necessary to implement your design
- Draw a truth table corresponding to this FSM, taking into account the inputs, outputs, current state, and next state.